Inter-arrival Time, Clustering, and Patterns

My last three posts in Poetics were personal reflections on recent artworks and books I’ve encountered. To be honest, writing under this category has been quite an enriching experience. At the same time, I have to admit that I did miss diving into probability distributions - finding counter-intuitive results and connecting them to principles and insights. So here we are again - this time exploring the human tendency to spot patterns where none exist and its implications for our broader search for unifying rules in life.
In the article series Binary Outcomes, Risk Aversion, Sorites Paradox (Part I and Part II), we built an intuition for the development of a Poisson distribution (hereon Poisson). The Poisson, defined by a single parameter lambda (λ) that is equal to distribution mean and variance, can be understood as a limiting case of the Binomial distribution when the following conditions are met:
-
The number of trials n is large (tending to infinity)
-
The probability of success p is small (tending to zero)
Under these conditions, λ can be approximated by n * p. If this still sounds a bit strange to you, I encourage you to revisit the article series above - not only to re-build your intuition for these distributions, but also to uncover non-obvious results that I believe influence risk aversion.
A Poisson is typically used to model independent events that occur randomly over time (see Chart 1). Some examples include modelling call arrivals at call centres, radioactive decay, mutation occurrences, and stock trade arrivals.
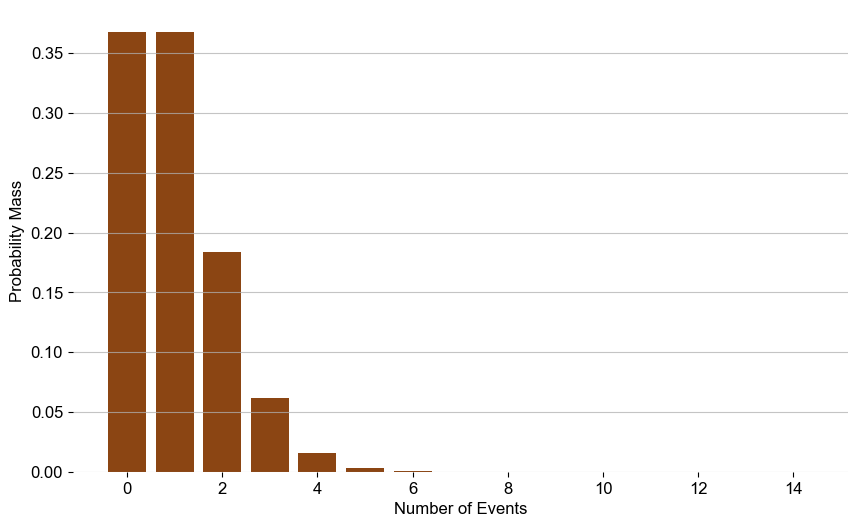
Building on this, while a Poisson models the number of events occurring in a given time interval, the inter-arrival time between events follows an Exponential Distribution (hereon Exponential). For a given Poisson, the inter-arrival time follows an Exponential characterized by λ (see Chart 2).
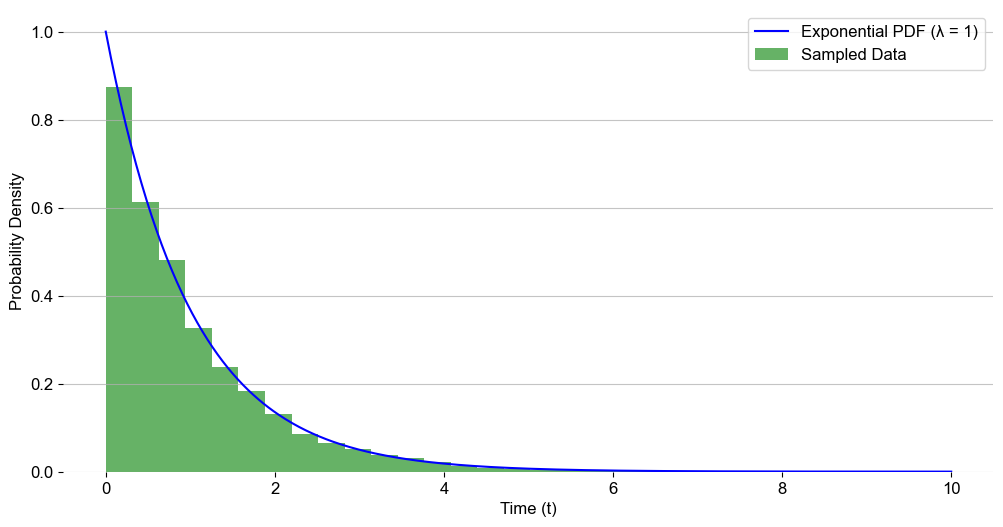
Now, what makes the Exponential interesting is its memoryless process. This means that the probability of an event occurring in the future is independent of how much time has passed since the occurrence of the last event. The memoryless property implies that the process “forgets” its past - prior waiting time doesn’t change future outcomes (this will be extremely important later).
In Chart 3, I’ve shown arrival of events that follow a Poisson (λ = 1). The orange lines represent the arrival of an event.
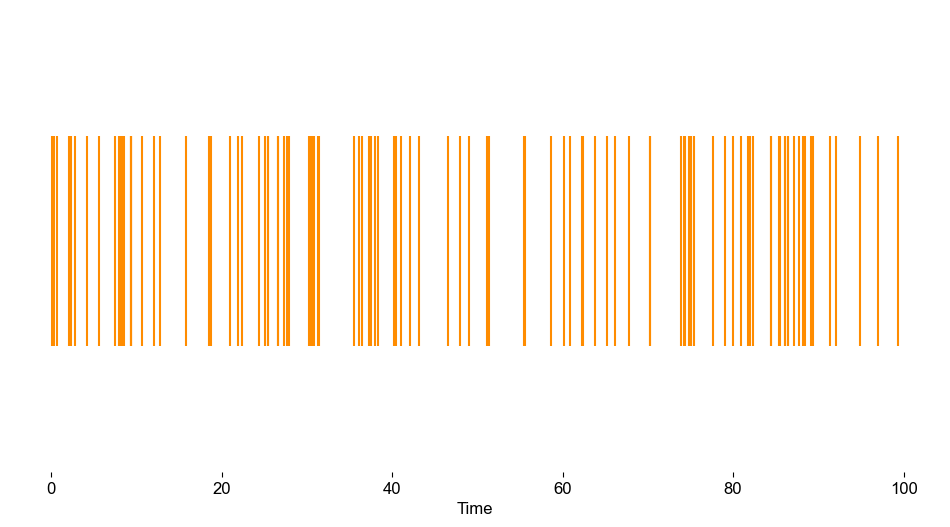
Now, for a moment, place yourself under a veil of ignorance - assume no prior knowledge of the Exponential’s memoryless nature. Looking at Chart 3, you’re asked whether the event arrivals exhibit a discernible pattern. Specifically, do you think the probability of the next event depends on how much time has passed since the last one? Before we delve into the question, take a moment to examine Chart 4, which features two panels:
Panel 1: This replicates the arrival times of events following an Exponential distribution, as seen earlier in Chart 3. The orange lines continue to represent the same moments when events arrive.
Panel 2: Here, I’ve added shaded regions in light blue to highlight regions where multiple events arrive within an interval of 1 second. The addition of these shaded areas in Panel 2 brings a new layer of visual insight.
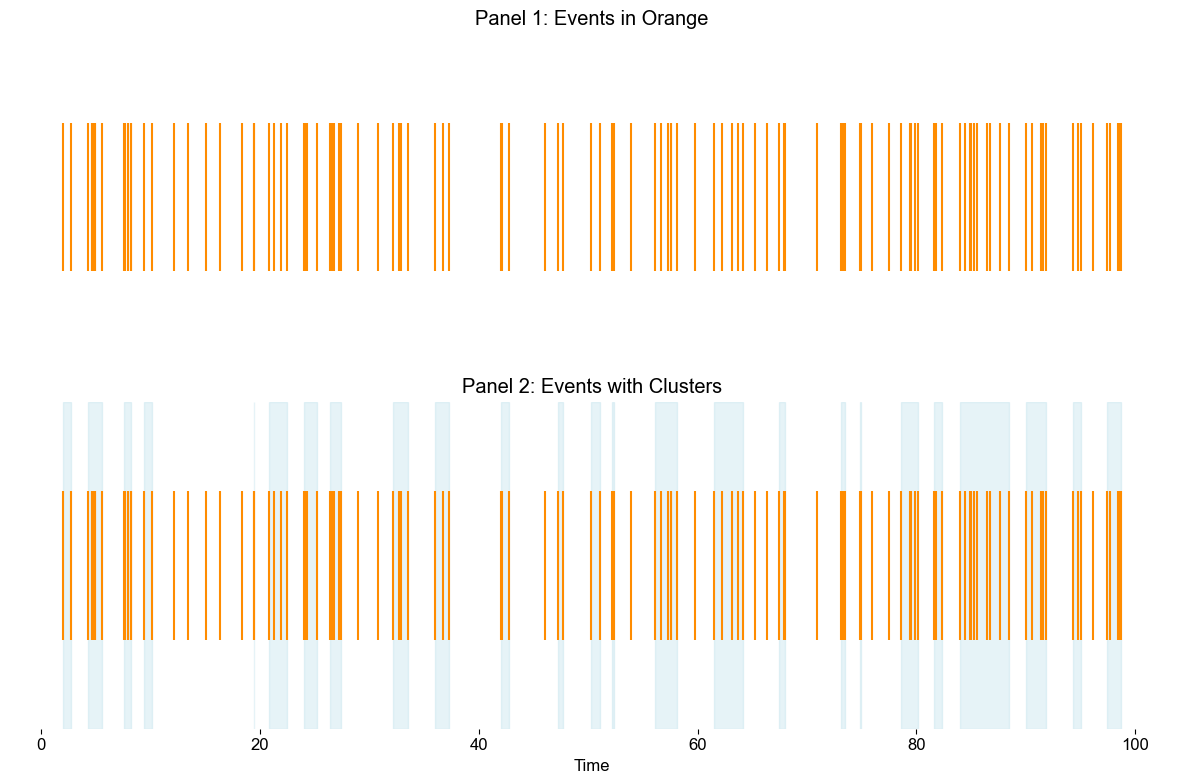
If you’re once again asked if you believe that the arrival of events follows a pattern, what would you say? From my perspective, there does seem to be some form of a pattern. This is quite important so let us now remove the veil of ignorance.
We technically know that inter-arrival times under an Exponential are independent. However, experientially, that doesn’t seem to be the case. Experientially, we observe clustering. In the context of inter-arrival times and event distributions, clustering refers to the tendency for events to occur in close temporal proximity to each other, followed by relatively longer gaps where no events occur. This creates a grouped appearance of events over time, rather than a uniform or evenly spaced pattern.
People often expect independent events to be evenly spaced, associating randomness with regularity. However, true randomness (such as that modeled by an Exponential) often results in uneven spacing and apparent clustering.
This classic example of the human tendency to see patterns where there are none often relates to our desire to make sense of an unpredictable world. Now there are multiple ways to slice this further. I’ve listed a couple of my favorite schools of thought below:
-
Kant believed that humans impose structures, such as time and space, onto raw experience to make sense of it. This imposition of order helps create a coherent experience of reality, even if it doesn’t perfectly reflect external truths. Kant’s ideas suggest that pattern-finding might be a necessary feature of human cognition that helps us navigate an otherwise overwhelming world.
-
Camus’ notion of the absurd explores the tension between our desire for meaning and the random nature of existence. This philosophical stance sees our pattern-spotting tendencies as an attempt to bridge this gap.
In navigating the murky waters of interpreting information - especially when it’s ambiguous or seemingly random - we find ourselves wrestling with a fundamental question: how do we separate signal (true patterns) from noise (randomness)? Taking this a step further, conditioned on us observing randomness, how do we even know that signals exist? This struggle is not just intellectual; it’s deeply existential. In my article Narratives, Chekhov’s Gun, and Agency, I explored how great stories embody the principle of narrative economy. Every detail and character serves a purpose, contributing meaningfully to the unfolding narrative. Anton Chekhov famously said, “If you hang a pistol on the wall in the first act, it should be fired by the second act.” In storytelling, nothing is accidental. Everything is connected.
Yet, juxtaposed with this narrative clarity is a sobering reality: life often defies such tidy coherence. Randomness clouds our interpretations, leaving us to wonder if the patterns we perceive are real or imagined. Here lies the impasse, the tension between our longing for meaning and the chaos of the unknown.
This challenge is more than a philosophical musing - it cuts to the very heart of why I write.
The core premise of my website is the belief in unifying rules, the idea that beneath the surface noise of life lies a coherent, rule-based meta-game.
In my first article, Origin, Meta-games and Unifying Rules, I wrote: “The desire to satiate thirst presupposes the existence of a source capable of quenching the thirst.”
By the same logic, I do believe that our innate drive to seek patterns suggests the existence of broader, perhaps transcendental, patterns - ones that may elude immediate experience.
While some of what we perceive as patterns might, in truth, be randomness masquerading as order, this does not deterministically nullify the existence of a grander structure; rather, it reframes the game we are playing. In Gradient Ascent, Global Maximum, and Complexity, I stated that life operates at multiple levels, each governed by its own set of rules. This helps me reason that while sub-levels of the game may be riddled with randomness, the overarching game may still be coherent and follow a pattern embedded with meaning (unifying rules).
In fact, if we believe that the overarching game is governed by unifying rules, then our task is even clearer: rigorously test the patterns we encounter, discern the signal from the noise, and re-orient our efforts to engage meaningfully at each level. To re-iterate, even when a specific sub-level seems random, this is no reason for despair.
The randomness of a part (sub-level) does not negate the order of the whole (overarching game).
And so, we return to the guiding principle: Absence of evidence is not evidence of absence.
Thank you for reading and see you next time! For those curious, the code for the charts can be found on GitHub.